在宇宙的深邃广袤中,星球不仅是天体物理学研究的重要对象,也是广义相对论应用的理想场景。爱因斯坦的广义相对论,通过其核心——爱因斯坦场方程,描述了物质如何影响时空的几何结构,进而影响物体的运动。在这篇文章中,我们将跟随《张朝阳的物理课》的脚步,深入探讨星球内部的爱因斯坦场方程,揭示其背后的物理原理和数学结构。
1. 爱因斯坦场方程简介
爱因斯坦场方程是广义相对论的核心,它将时空的曲率与物质和能量的分布联系起来。方程的一般形式为:
\[ G_{\mu\nu} = 8\pi G T_{\mu\nu} \]
其中,\( G_{\mu\nu} \) 是爱因斯坦张量,描述了时空的曲率;\( T_{\mu\nu} \) 是能量动量张量,表示物质的能量和动量分布;\( G \) 是引力常数。这个方程表明,时空的曲率是由物质和能量的分布决定的。
2. 星球内部的特殊情况
在星球内部,物质分布通常是球对称的。这种对称性简化了爱因斯坦场方程,使其可以解析求解。对于一个静态、球对称的星球,我们可以使用史瓦西度规来描述其内部的时空结构:
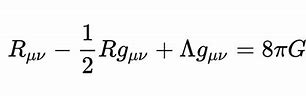
\[ ds^2 = e^{2\Phi(r)} dt^2 e^{2\Lambda(r)} dr^2 r^2 d\Omega^2 \]
其中,\(\Phi(r)\) 和 \(\Lambda(r)\) 是依赖于半径 \( r \) 的函数,\( d\Omega^2 \) 是球面上的角度元素。
3. 推导星球内部的爱因斯坦场方程
为了推导星球内部的爱因斯坦场方程,我们需要将史瓦西度规代入爱因斯坦场方程中,并利用球对称性进行简化。这个过程涉及到复杂的数学运算,包括计算爱因斯坦张量和能量动量张量。
通过这些计算,我们可以得到两个关键的方程:
\[ \frac{d\Phi}{dr} = \frac{G(4\pi r^3 P M)}{r(r 2GM)} \]
\[ \frac{dP}{dr} = (\rho P)(\frac{d\Phi}{dr}) \]
其中,\( \rho \) 是物质的密度,\( P \) 是压强,\( M \) 是到半径 \( r \) 为止的物质总质量。
4. 物理意义和应用
这两个方程描述了星球内部的时空结构和物质状态。第一个方程表明,时空的引力势 \(\Phi(r)\) 与物质的分布密切相关。第二个方程,称为托尔曼奥本海默沃尔科夫方程,描述了物质内部的压强如何随半径变化,这是理解星球内部结构和稳定性的关键。
5. 结论
通过《张朝阳的物理课》的推导,我们不仅深入理解了爱因斯坦场方程在星球内部的特殊形式,还揭示了星球内部时空结构与物质分布之间的深刻联系。这些知识不仅对基础物理学有重要意义,也对天体物理学、宇宙学乃至地球物理学等领域有着深远的影响。
通过这篇文章,我们希望读者能够更加欣赏到广义相对论的数学之美和物理之深,同时也激发对宇宙奥秘的进一步探索。











